PID Controller
https://www.ni.com/en-us/innovations/white-papers/06/pid-theory-explained.html
PID Controller are popular because of
1. Functional simplicity
2. Robust performance in a wide range of operating conditions
3. Simple operation
PID algorithm consists of three basic coefficients; proportional, integral and derivative which are varied to get optimal response.
Idea behind a PID controller is to read a sensor, then compute the desired actuator output by calculating proportional, integral, and derivative responses and summing those three components to compute the output.
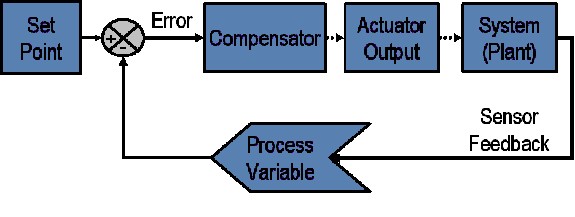
Figure 1: Block diagram of a typical closed loop system.
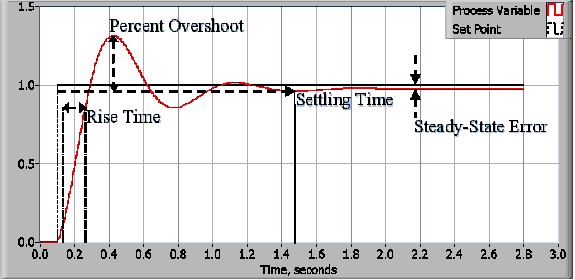
Figure 2: Response of a typical PID closed loop system.
PID Controller are popular because of
1. Functional simplicity
2. Robust performance in a wide range of operating conditions
3. Simple operation
PID algorithm consists of three basic coefficients; proportional, integral and derivative which are varied to get optimal response.
Idea behind a PID controller is to read a sensor, then compute the desired actuator output by calculating proportional, integral, and derivative responses and summing those three components to compute the output.
In a typical control system, the process variable is the system parameter that needs to be controlled, such as temperature (ºC), pressure (psi), or flow rate (liters/minute). A sensor is used to measure the process variable and provide feedback to the control system. The set point is the desired or command value for the process variable, such as 100 degrees Celsius in the case of a temperature control system. At any given moment, the difference between the process variable and the set point is used by the control system algorithm (compensator), to determine the desired actuator output to drive the system (plant). For instance, if the measured temperature process variable is 100 ºC and the desired temperature set point is 120 ºC, then the actuator output specified by the control algorithm might be to drive a heater. Driving an actuator to turn on a heater causes the system to become warmer, and results in an increase in the temperature process variable. This is called a closed loop control system, because the process of reading sensors to provide constant feedback and calculating the desired actuator output is repeated continuously and at a fixed loop rate as illustrated in figure 1.
In many cases, the actuator output is not the only signal that has an effect on the system. For instance, in a temperature chamber there might be a source of cool air that sometimes blows into the chamber and disturbs the temperature.Such a term is referred to as disturbance. We usually try to design the control system to minimize the effect of disturbances on the process variable.
In many cases, the actuator output is not the only signal that has an effect on the system. For instance, in a temperature chamber there might be a source of cool air that sometimes blows into the chamber and disturbs the temperature.Such a term is referred to as disturbance. We usually try to design the control system to minimize the effect of disturbances on the process variable.

Figure 1: Block diagram of a typical closed loop system.
Control system performance is often measured by applying a step function as the set point command variable, and then measuring the response of the process variable. Commonly, the response is quantified by measuring defined waveform characteristics.
Rise Time is the amount of time the system takes to go from 10% to 90% of the steady-state, or final, value.
Percent Overshoot is the amount that the process variable overshoots the final value, expressed as a percentage of the final value.
Settling time is the time required for the process variable to settle to within a certain percentage (commonly 5%) of the final value.
Steady-State Error is the final difference between the process variable and set point. Note that the exact definition of these quantities will vary in industry and academia.

Figure 2: Response of a typical PID closed loop system.
Often times, there is a disturbance in the system that affects the process variable or the measurement of the process variable. It is important to design a control system that performs satisfactorily during worst case conditions. The measure of how well the control system is able to overcome the effects of disturbances is referred to as the disturbance rejection of the control system.
In some cases, the response of the system to a given control output may change over time or in relation to some variable. A nonlinear system is a system in which the control parameters that produce a desired response at one operating point might not produce a satisfactory response at another operating point.
The measure of how well the control system will tolerate disturbances and nonlinearities is referred to as the robustness of the control system.
Some systems exhibit an undesirable behavior called deadtime. Deadtime is a delay between when a process variable changes, and when that change can be observed. Deadtime can also be caused by a system or output actuator that is slow to respond to the control command.
PID Theory
Proportional Response
The proportional component depends only on the difference between the set point and the process variable. This difference is referred to as the Error term. The proportional gain (Kc) determines the ratio of output response to the error signal. In general, increasing the proportional gain will increase the speed of the control system response. However, if the proportional gain is too large, the process variable will begin to oscillate. If Kc is increased further, the oscillations will become larger and the system will become unstable and may even oscillate out of control.
The proportional component depends only on the difference between the set point and the process variable. This difference is referred to as the Error term. The proportional gain (Kc) determines the ratio of output response to the error signal. In general, increasing the proportional gain will increase the speed of the control system response. However, if the proportional gain is too large, the process variable will begin to oscillate. If Kc is increased further, the oscillations will become larger and the system will become unstable and may even oscillate out of control.

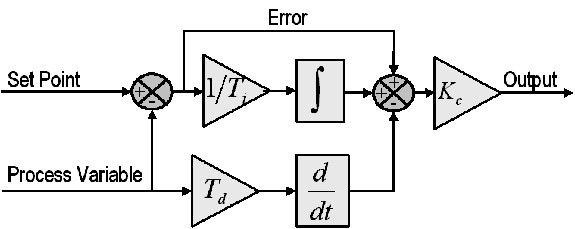
Figure 4: Block diagram of a basic PID control algorithm.
Integral Response
The integral component sums the error term over time. The result is that even a small error term will cause the integral component to increase slowly. The integral response will continually increase over time unless the error is zero, so the effect is to drive the Steady-State error to zero. Steady-State error is the final difference between the process variable and set point. A phenomenon called integral windup results when integral action saturates a controller without the controller driving the error signal toward zero.
The integral component sums the error term over time. The result is that even a small error term will cause the integral component to increase slowly. The integral response will continually increase over time unless the error is zero, so the effect is to drive the Steady-State error to zero. Steady-State error is the final difference between the process variable and set point. A phenomenon called integral windup results when integral action saturates a controller without the controller driving the error signal toward zero.
- Integral wind-up occurs when the summation within the integral increases beyond the saturation limit of the actuators it’s controlling, causing reduced performance.
Derivative Response
The derivative component causes the output to decrease if the process variable is increasing rapidly. The derivative response is proportional to the rate of change of the process variable. Increasing the derivative time (Td) parameter will cause the control system to react more strongly to changes in the error term and will increase the speed of the overall control system response. Most practical control systems use very small derivative time (Td), because the Derivative Response is highly sensitive to noise in the process variable signal. If the sensor feedback signal is noisy or if the control loop rate is too slow, the derivative response can make the control system unstable.
The derivative component causes the output to decrease if the process variable is increasing rapidly. The derivative response is proportional to the rate of change of the process variable. Increasing the derivative time (Td) parameter will cause the control system to react more strongly to changes in the error term and will increase the speed of the overall control system response. Most practical control systems use very small derivative time (Td), because the Derivative Response is highly sensitive to noise in the process variable signal. If the sensor feedback signal is noisy or if the control loop rate is too slow, the derivative response can make the control system unstable.
Tuning
The process of setting the optimal gains for P, I and D to get an ideal response from a control system is called tuning. There are different methods of tuning of which the “guess and check” method and the Ziegler Nichols method will be discussed.
The gains of a PID controller can be obtained by trial and error method.
As one increases the proportional gain, the system becomes faster, but care must be taken not make the system unstable.
Once P has been set to obtain a desired fast response, the integral term is increased to stop the oscillations. The integral term reduces the steady state error, but increases overshoot. Some amount of overshoot is always necessary for a fast system so that it could respond to changes immediately.
The derivative term is increased until the loop is acceptably quick to its set point. Increasing derivative term decreases overshoot and yields higher gain with stability but would cause the system to be highly sensitive to noise. Often times, engineers need to tradeoff one characteristic of a control system for another to better meet their requirements.
Comments
Post a Comment